Antwort Wie erkennt man eine rationale Zahl? Weitere Antworten – Wie erkenne ich ob eine Zahl rational oder irrational ist

Rationale und irrationale Zahlen

Rationale Zahlen kannst du als Bruch aus ganzen Zahlen oder als abbrechende oder periodische Dezimalzahl (Kommazahl) schreiben. Hat deine Dezimalzahl dagegen unendliche viele Nachkommastellen und wird nicht periodisch, ist sie eine irrationale Zahl.Eine Zahl ist rational, wenn du sie als einen Bruch aus zwei ganzen Zahlen a und b schreiben kannst. Vergiss nicht, dass auch ganze Zahlen und Dezimalzahlen zu der Menge der rationalen Zahlen gehören. a nennst du den Zähler und b den Nenner.Irrationale Zahlen sind Dezimalzahlen mit unendlich vielen Stellen nach dem Komma, die sich nicht periodisch wiederholen. Hierzu gehören z.B. die Wurzeln aus natürlichen Zahlen, die keine Quadratzahlen sind. Auch die Kreiszahl π=3.14159… ist eine irrationale Zahl – sie ist keine periodische Dezimalzahl.

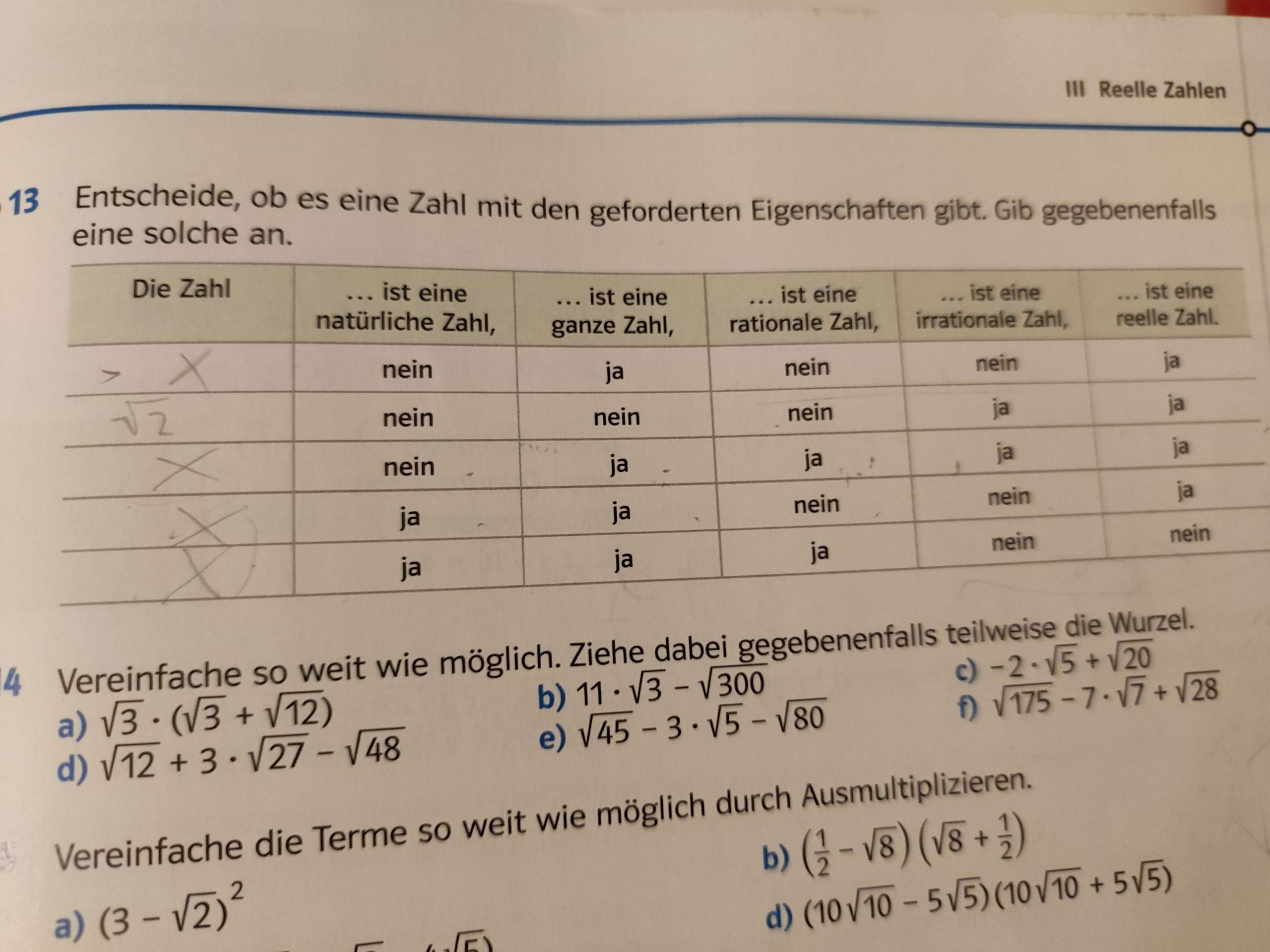
Ist 12 eine rationale Zahl : Rationale Zahlen auf dem Zahlenstrahl

Jede natürliche Zahl ist eine rationale Zahl, zum Beispiel 11. Jede ganze Zahl ist auch eine rationale Zahl, zum Beispiel −3.

Ist diese Zahl rational oder irrational

Rationale Zahlen können als jede Zahl oder jeder Wert definiert werden, der als Bruch oder Verhältnis geschrieben werden kann. Jede Zahl, die nicht als Bruch geschrieben werden kann, ist irrational.

Welche sind die rationale Zahlen : Rationale Zahlen sind eine elementare Zahlenmenge, die alle natürlichen Zahlen, ganzen Zahlen, Brüche und Dezimalzahlen, die sich als Bruch darstellen lassen, enthält. Sie sind wichtige Bestandteile im Alltag und in verschiedenen Berufsbereichen.

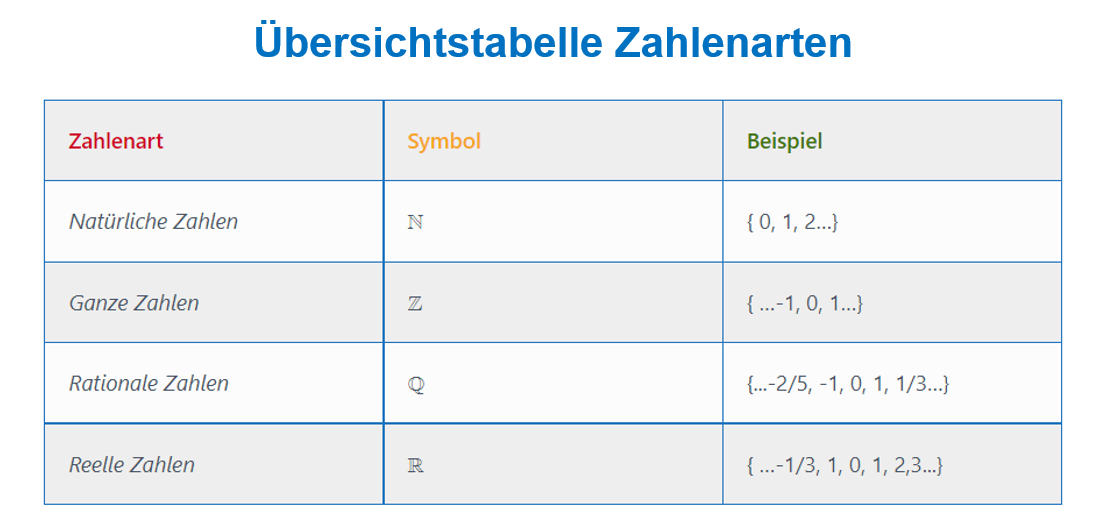
Rationale (gebrochene) Zahlen

Hierbei ist es egal, ob der Bruch als Bruch geschrieben wird oder es sich um eine Dezimalzahl handelt, also der Bruch ausgeschrieben wurde, zum Beispiel 0,25. Diese Zahlen gehören alle zu den rationalen Zahlen. Das Symbol der rationalen Zahlen ist das \Large{ℚ}.

Eine ganze Zahl kann als Bruch geschrieben werden, indem man ihr den Nenner Eins gibt, sodass jede ganze Zahl eine rationale Zahl ist . Eine abschließende Dezimalzahl kann mithilfe von Stellenwerteigenschaften als Bruch geschrieben werden. Zum Beispiel 3,75 = drei und fünfundsiebzig Hundertstel oder 3 75 100 , was dem unechten Bruch entspricht.

Woher wissen wir, dass irrationale Zahlen niemals enden

Im Fall irrationaler Zahlen endet die Dezimalentwicklung nicht und endet auch nicht mit einer sich wiederholenden Folge . Beispielsweise beginnt die Dezimaldarstellung von π mit 3,14159, aber keine endliche Anzahl von Ziffern kann π exakt darstellen und es wiederholt sich auch nicht.Die reellen Zahlen, die nicht in der Form p/q ausgedrückt werden können, wobei p und q ganze Zahlen sind und q ≠ 0, werden als irrationale Zahlen bezeichnet. Beispielsweise sind √2 und √ 3 usw. irrational. Während jede Zahl, die in der Form p/q dargestellt werden kann, so dass p und q ganze Zahlen sind und q ≠ 0, als rationale Zahl bekannt ist.Was ist eine rationale Zahl Beispiel Jede natürliche Zahl ist eine rationale Zahl (z.B. 13). Jede Ganze Zahl ist eine rationale Zahl (z.B. -7). Jeder dieser Zahlen kann als unechter Bruch dargestellt werden und ist deswegen auch eine rationale Zahl.

Als Rationale Zahlen bezeichnet man alle negativen und positiven Zahlen. Dazu gehören auch Brüche und Kommazahlen. Betrachtet man einen Zahlenstrahl, so liegen die negativen Zahlen links von der Null und die positiven Zahlen rechts von der Null.

Ist 0,59136363636363636 rational oder irrational : Von Experten verifizierte Antwort

Die angegebene wiederkehrende Dezimalzahl 0,59136363636 ist eine rationale Zahl . Angesichts dessen: Um zu bestimmen, ob der gegebene wiederkehrende Dezimalwert rational oder irrational ist.

Welche Zahl ist irrational : Die reellen Zahlen, die nicht in der Form p/q ausgedrückt werden können, wobei p und q ganze Zahlen sind und q ≠ 0, werden als irrationale Zahlen bezeichnet. Beispielsweise sind √2 und √ 3 usw. irrational. Während jede Zahl, die in der Form p/q dargestellt werden kann, so dass p und q ganze Zahlen sind und q ≠ 0, als rationale Zahl bekannt ist.

Was sind rationale Zahlen für Kinder erklärt

Rationale Zahlen sind eine elementare Zahlenmenge, die alle natürlichen Zahlen, ganzen Zahlen, Brüche und Dezimalzahlen, die sich als Bruch darstellen lassen, enthält. Sie sind wichtige Bestandteile im Alltag und in verschiedenen Berufsbereichen.

Wenn wir diese Fakten kombinieren, kommen wir zu dem Schluss, dass An(b) A n ( b ) eine ganze Zahl sein muss. Der Widerspruch zwischen dieser Tatsache und der oben bewiesenen Tatsache, dass nämlich 0<An(b)<1 0 < A n ( b ) < 1 für alle n≥1 n ≥ 1 und alle ausreichend großen n , beweist, dass π irrational ist .Der tatsächliche Wert von π hingegen ist 3,141516…….. was bedeutet, dass die Werte nach der Dezimalzahl kein Ende haben, daher sind wir nicht in der Lage, den tatsächlichen Wert von π zu finden und ihn daher nicht darzustellen eine Zahlenlinie und außerdem können wir sie nicht in der Form p/q darstellen , deshalb ist sie eine irrationale Zahl.

Wie beweisen Sie, dass √5 irrational ist : Der für die Wurzel aus 5 erhaltene Wert endet nicht und dehnt sich nach dem Dezimalpunkt immer weiter aus . Dies erfüllt die Bedingung, dass √5 eine irrationale Zahl ist. Daher ist √5 eine irrationale Zahl.