Antwort Wie berechne ich das unbestimmte Integral? Weitere Antworten – Wie berechnet man das unbestimmte Integral

Wie berechne ich das unbestimmte Integral Das unbestimmte Integral ist die Menge aller Stammfunktionen einer Funktion f(x). Um das unbestimmte Integral einer Funktion f(x) zu berechnen, muss die Stammfunktion gebildet und eine Konstante C addiert werden.Den Wert eines bestimmten Integrals über eine Funktion f berechnet man, indem man ihre Stammfunktion an den beiden Integrationsgrenzen auswertet und die Differenz der beiden bildet ("obere Grenze minus untere Grenze"). Die Konstante C, die in der allgemeinen Stammfunktion steht, fällt hierbei weg (hebt sich auf).Um ein bestimmtes Integral zu berechnen, gehst du so vor:

1. Schritt 1: Berechne die Stammfunktion F(x) und schreibe Sie in eckige Klammern.
2. Schritt 2: Setze die Integrationsgrenzen a und b in F(x) ein.
3. Schritt 3: Ziehe F(a) von F(b) ab.

Was ist der Unterschied zwischen bestimmten und unbestimmten Integralen : Bestimmtes und unbestimmtes Integral Definition

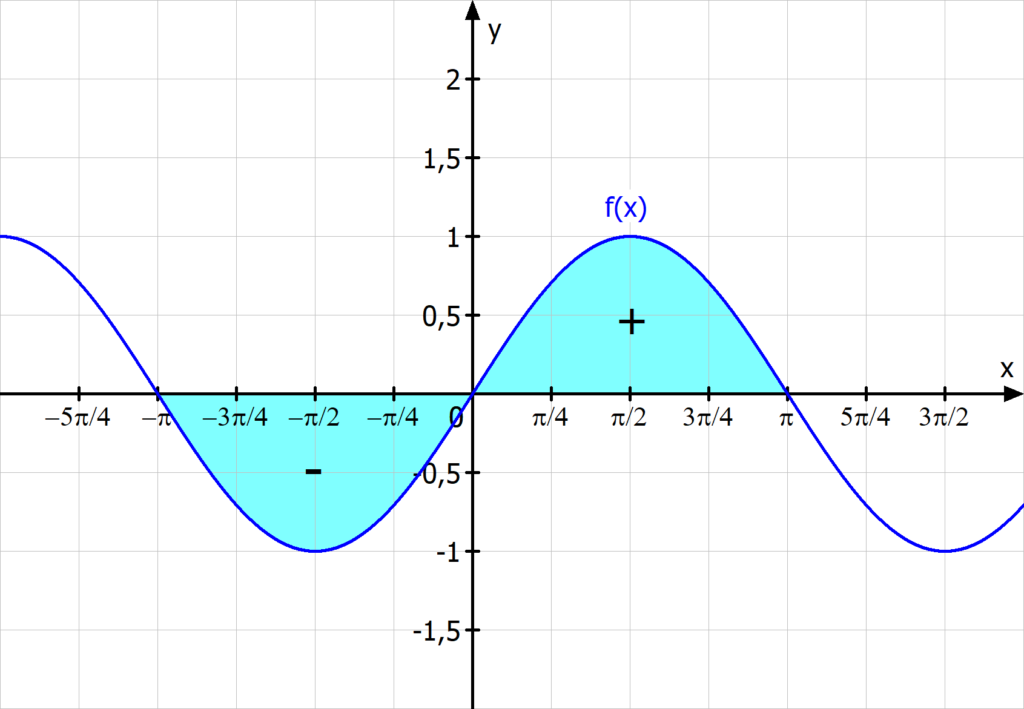
Beim bestimmten Integral berechnest du den Flächeninhalt einer Funktion (es gibt zwei Integrationsgrenzen). Beim unbestimmten Integral bestimmst du alle Stammfunktionen einer Funktion (hier gibt es keine Integrationsgrenzen).

Was ist das unbestimmte Integral

Bestimmtes und unbestimmtes Integral einfach erklärt

Ein unbestimmtes Integral hingegen hat keine Integralgrenzen. Du berechnest es, indem du die sogenannte Stammfunktion von f(x) ermittelst. Davon gibt es immer unendlich viele. Die Menge aller Stammfunktionen nennst du dann unbestimmtes Integral.

Ist das unbestimmte Integral die Stammfunktion : Ein bestimmtes Integral beschreibt einen orientierten Flächeninhalt, ist also ein einfacher Zahlenwert. Ein unbestimmtes Integral ist die Menge aller sogenannten Stammfunktionen.

Du integrierst eine Konstante a, indem du an die Konstante ein x anhängst und + c schreibst. Das c steht für eine beliebige Zahl. Du integrierst eine Potenzfunktion nach der Variablen x, indem du den Exponenten um 1 erhöhst. Anschließend teilst du die Funktion durch den neuen, um 1 erhöhten Exponenten.

A ( x ) := ∫ a x f ( x ) d x eine Stammfunktion A(x) zu f(x) definiert. A(x) wird auch Integralfunktion und Flächeninhaltsfunktion genannt.

Kann jede Funktion integriert werden

Achtung: Jede stetige Funktion ist integrierbar, die Umkehrung gilt dagegen nicht: es gibt auf einem Intervall integrierbare Funktionen, die dort nicht (überall) stetig sind!Die Integralrechnung ist ein Teil der Analysis. Sie wird genutzt, um Flächeninhalte und Volumen zu berechnen, und ist eng verwandt mit der Differentialrechnung. In der Integralrechnung bildest du bestimmte und unbestimmte Integrale. Dazu musst du die Stammfunktion einer Funktion bestimmen.Der Hauptsatz der Differential- und Integralrechnung

Das bedeutet: F ' ( x ) = f ( x ) F'(x)=f(x) F'(x)=f(x)

Die Differentialrechnung beschäftigt sich mit dem Änderungsverhalten einer Funktion an einem bestimmten Punkt. Das Änderungsverhalten wird mithilfe des Differentialquotienten bestimmt und wird auch als Ableitung der Funktion bezeichnet.

Wann ist ein Integral integrierbar : das Riemann-Integral von f über Q. Eine beschränkte Funktion f : Q → R ist genau dann Riemann-integrierbar, wenn es zu jedem ε > 0 eine Zerlegung Z von Q mit O(f,Z) − U(f,Z) < ε.

Wann ist eine Funktion nicht integrierbar : Die Betrachtung von Integralen mit entweder unbeschränktem Integrationsintervall oder unbeschränktem Integranden führt zum Begriff des uneigentlichen Integrals. Funktionen, deren Integrale sich nicht durch elementare Funktionen ausdrücken lassen, werden nicht geschlossen integrierbar genannt.

Was berechnet man mit dem Hauptsatz der Integralrechnung

Der Hauptsatz ermöglicht die effektive Berechnung bestimmter Integrale mithilfe der Stammfunktion. Beispiel: Das bestimmte Integral ∫ 2 4 ( x 2 − 2 x ) d x ist zu berechnen. (Auf die Angabe von C wird in der Regel verzichtet, da diese Konstante beim Subtrahieren ohnehin wegfiele.)

In Worten: Die Ableitung der Integralfunktion ist gleich der Integrandenfunktion an der oberen Integrationsgrenze. Hinweis: Mit d d x ( ⋯ ) wird die Ableitung des Ausdrucks in der Klammer nach x bezeichnet.Hier wird im Differentialquotienten das x durch x₀+h, wofür dann der Grenzwert h ⟶ 0 berechnet wird. Die Ableitung entspricht dabei also folgender Formel: f'(x)=(f(x+h)-f(x)):h, wobei h gegen 0 läuft.

Was bedeutet DF in Mathe : Ein Differential (oder Differenzial) bezeichnet in der Analysis den linearen Anteil des Zuwachses einer Variablen oder einer Funktion und beschreibt einen unendlich kleinen Abschnitt auf der Achse eines Koordinatensystems.