Antwort Welche Funktionen sind konvex? Weitere Antworten – Wann ist die Funktion konvex

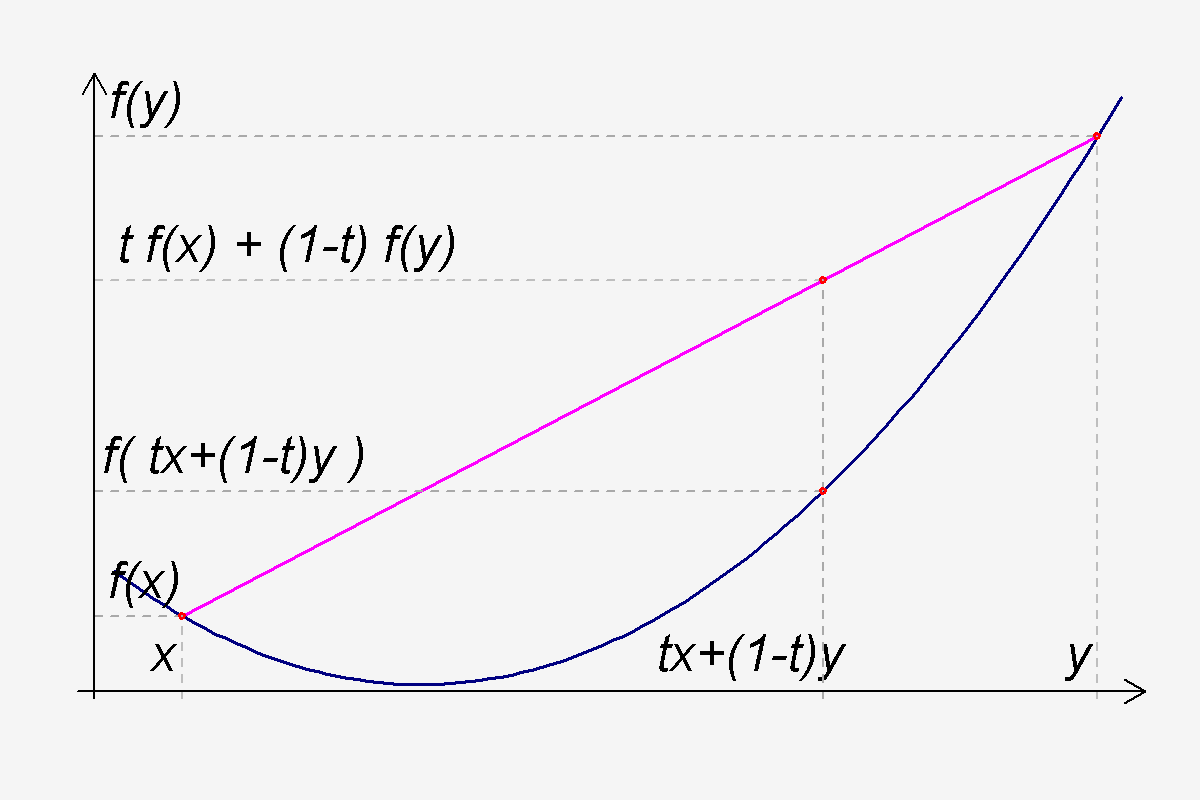
In der Analysis heißt eine reellwertige Funktion konvex (lateinisch convexus ‚nach oben oder unten gewölbt'), wenn ihr Graph unterhalb jeder Verbindungsstrecke zweier seiner Punkte liegt.Jede lineare Funktion ist konvex und konkav. Die Sinus-, Cosinus- und Tangensfunktion sind weder konvex noch konkav. Sind f und g zwei konvexe (konkave) Funktionen, so ist auch jede Linearkombination af+bg mit a,b є R+ wieder konvex (konkav).Eine Funktion ϕ : (a, b) → R heißt konvex, wenn ϕ((1 − λ)x + λy) ≤ (1 − λ)ϕ(x) + λϕ(y) für alle x, y ∈ (a, b) und 0 ≤ λ ≤ 1 . Bemerkung. Ist ϕ : (a, b) → R konvex, dann ist ϕ stetig auf (a, b) .

Was ist konvex in Mathe : In der Mathematik heißt eine geometrische Figur oder allgemeiner eine Teilmenge eines euklidischen Raums konvex, wenn für je zwei beliebige Punkte, die zur Menge gehören, auch stets deren Verbindungsstrecke ganz in der Menge liegt.

Wann konkav und wann konvex

konkav und konvex ist ein Begriffspaar, das die Gestalt von Phänomenen beschreibt. Dabei bedeutet konkav (von lateinisch concavus ‚gewölbt') „nach innen gewölbt“ und konvex (von lateinisch convexus ‚nach oben oder unten gewölbt') „nach außen gewölbt“.

Wie merkt man sich konkav und konvex : "War das Mädchen brav, bleibt der Bauch konkav. Hatte sie Sex, wird der Bauch konvex." Damit vergessen wir nie wieder den Unterschied: konkav – nach innen gewölbt, konvex – nach außen gewölbt.

Die Funktion ist konvex, wenn ihr Graph unterhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Die Funktion ist konkav, wenn ihr Graph oberhalb jeder Verbindungsstrecke zweier seiner Punkte liegt.

Liegt der Graph der Funktion stets unterhalb der Tangente bzw. liegt die Sekante stets unterhalb der Funktionskurve, so ist die Funktion konkav gekrümmt. Entsprechend gilt für konvexe Funktionen, dass der Graf der Funktion stets überhalb der Tangente und unterhalb der Sekante liegt.

Welche Funktionen sind alle stetig

Stetige Funktionen

Stetige Funktionen	Beispiel
Wurzelfunktion	f ( x ) = x m n
Trigonometrische Funktion	f ( x ) = sin ⁡ ( x ) ; g ( x ) = cos ⁡ ( x ) ; h ( x ) = tan ⁡
Logarithmusfunktion	f ( x ) = log a ⁡
Exponentialfunktion	f ( x ) = a x

Eine Funktion ist genau dann quasi-konkav, wenn die Niveaumengen {x−|f(x−)≥k} { x _ | f ( x _ ) ≥ k } für alle k∈R k ∈ R konvex sind. Im eindimensionalen Fall ist dies gleichbedeutend mit der Aussage, dass die Niveaumenge ein Intervall ist. Die Konvexitätseigenschaft kann bei monotonen Transformationen verlorengehen.Konkav steht für: konkav, nach innen gewölbt, siehe konkav und konvex. konkav, Eigenschaft einer mathematischen Funktion, siehe konvexe und konkave Funktionen. konkav, nach innen gewölbte Linsenoberflächen, siehe Linse (Optik) #Verschiedene Linsenformen.

Die Funktion ist konvex, wenn ihr Graph unterhalb jeder Verbindungsstrecke zweier seiner Punkte liegt. Die Funktion ist konkav, wenn ihr Graph oberhalb jeder Verbindungsstrecke zweier seiner Punkte liegt.

Wie bestimmt man Konvexität : Mathematisch ist die Konvexität die zweite Ableitung (die Krümmung) des Börsenkurses nach der Rendite dividiert durch den Börsenkurs.

Wie finde ich heraus ob eine Funktion stetig ist : Eine Funktion ist stetig, wenn der Graph der Funktion im Definitionsbereich nahtlos gezeichnet werden kann. Anders ausgedrückt: Der Graph muss in jedem zusammenhängenden Teilintervall aus dem Definitionsbereich nahtlos gezeichnet werden können.

Wie überprüft man ob eine Funktion stetig ist

Eine Funktion f : D → R heißt (punktweise) stetig, wenn sie in allen Punkten a ∈ D stetig ist. D := {x ∈ D | g(x) = 0} setzt. Die Verkettung stetiger Funktionen ist stetig, d.h.: Sind f : D → R und g : E → R zwei Funktionen mit f(D) ⊆ E und ist f in x0 ∈ D und g in y0 = f(x0) stetig, so ist g ◦ f in x0 stetig.

Eine Funktion f : D → R heißt (punktweise) stetig, wenn sie in allen Punkten a ∈ D stetig ist. D := {x ∈ D | g(x) = 0} setzt. Die Verkettung stetiger Funktionen ist stetig, d.h.: Sind f : D → R und g : E → R zwei Funktionen mit f(D) ⊆ E und ist f in x0 ∈ D und g in y0 = f(x0) stetig, so ist g ◦ f in x0 stetig.Eine Funktion ist stetig, wenn der Graph der Funktion im Definitionsbereich nahtlos gezeichnet werden kann. Anders ausgedrückt: Der Graph muss in jedem zusammenhängenden Teilintervall aus dem Definitionsbereich nahtlos gezeichnet werden können.

Wie überprüft man Stetigkeit einer Funktion : Um die Funktion an einer Nahtstelle auf Stetigkeit zu überprüfen, setzt man diese in die Funktionsterme der beiden angrenzenden Abschnitte ein. Ergeben sich unterschiedliche Termwerte, so liegt eine Unstetigkeitsstelle vor. Ansonsten ist die Funktion dort stetig.