Antwort Kann man den Sinussatz auch umdrehen? Weitere Antworten – Kann man den Sinussatz umdrehen

Man kann den Sinussatz auch umstellen und wie folgt schreiben: s i n ( α ) ⋅ b = s i n ( β ) ⋅ a sin(\alpha) \cdot b = sin(\beta) \cdot a sin(α)⋅b= sin(β)⋅a.Das heißt, das Verhältnis des Sinus eines Winkels zu seiner Gegenseite ist in jedem Dreieck gleich. Das heißt, die Verhältnisse zwischen allen Winkeln und ihren gegenüberliegenden Seitenlängen sind direkt proportional zueinander. Aber natürlich können wir die Gleichung auch umdrehen und es würde immer noch funktionieren!Der Sinussatz gibt eine Beziehung zwischen den Winkeln eines allgemeinen Dreiecks und den gegenüberliegenden Seiten an. Das bedeutet: Wenn du in einem allgemeinen Dreieck von je zwei Winkeln und den entsprechend gegenüberliegenden Seiten drei Größen kennst, kannst die fehlende vierte Größe berechnen.

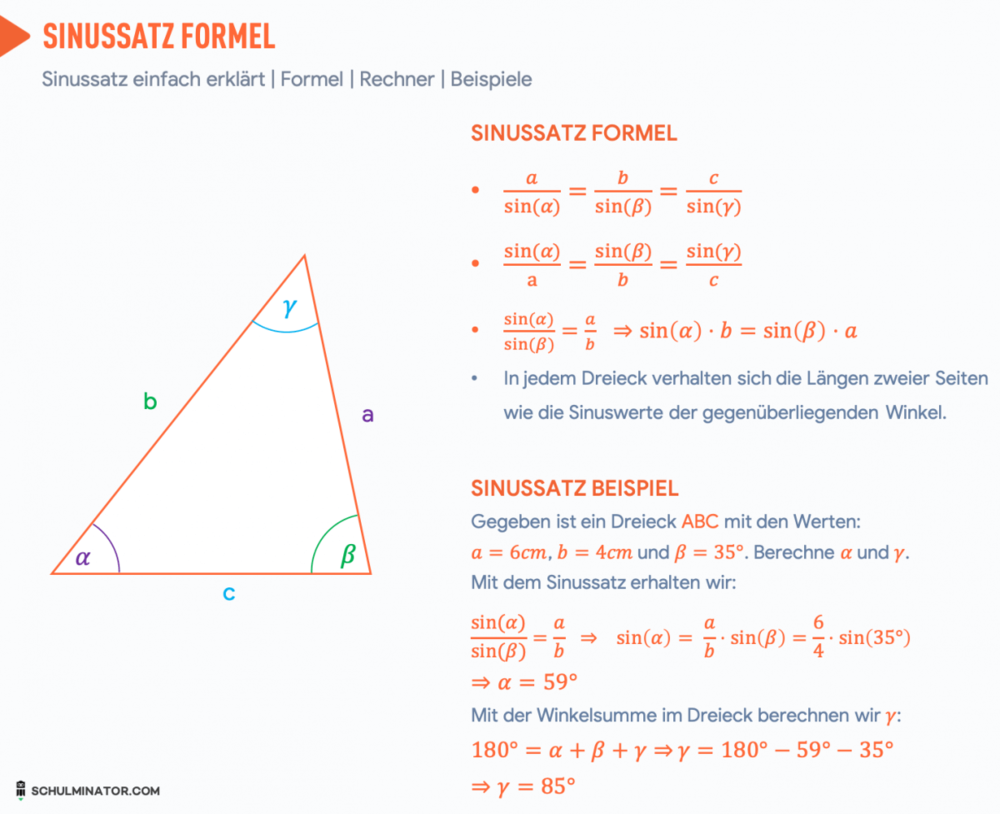
Kann man mit dem Sinussatz Seiten berechnen : Mit dem Sinussatz kannst Du Seiten und Winkel in jedem Dreieck bestimmen, solange Du nur ein „Seiten-Winkel-Paar“ und eine weitere Größe kennst. An diesem Dreieck sind die drei Seiten und deren gegenüberliegenden Winkel dargestellt.

Was sind die drei Sinusgesetze

Das Sinusgesetz wird im Detail wie folgt erklärt: In einem Dreieck ist die Seite „a“, geteilt durch den Sinus des Winkels A, gleich der Seite „b“, geteilt durch den Sinus des Winkels B, gleich der Seite „c“, geteilt durch den Sinus des Winkels C .

Warum gilt der Sinussatz : Der Sinussatz verbindet gegenüberliegende Größen (Seiten und Winkel) im allgemeinen Dreieck. Sind zwei einander gegenüberliegende Größen gegeben, so kann zu einer dritten die gegenüberliegende Größe berechnet werden. Der Sinussatz verbindet gegenüberliegende Größen (Seiten und Winkel) im allgemeinen Dreieck.

Dann ist es nur noch eine Frage der Verwendung der Algebra. also sin(alpha) = x/B und sin(beta) = x/A. Wenn man also weniger mathematisch betrachtet ein Dreieck in zwei rechtwinklige Dreiecke aufteilt, ergibt sich, dass die Senkrechte sowohl A * sin(beta) als auch B * sin(alpha) ist . Dann können Sie dies weiter umgestalten, um das Sinusgesetz, wie wir es kennen, zu erhalten.

Was besagt der Sinussatz

• müssen mindestens 3 Größen (Seitenlängen bzw. Winkel) bekannt sein und.
• unter den gegebenen Größen müssen eine Seitenlänge und der gegenüberliegende Winkel sein.

Kann man mit 2 Winkel eine Seite berechnen

Mit dem Sinussatz kannst du aus zwei Winkeln und der Länge einer der beiden gegenüberliegenden Seiten (sww) die Länge der anderen gegenüberliegenden Seite berechnen.Der Sinus ist nur im rechtwinkligen Dreieck definiert als Gegenkathete geteilt durch Hypotenuse. (Ausführliche Informationen und Übungsmaterial zum Sinus im rechtwinkligen Dreieck findest du auf der Seite LEARNZEPT.de.) Der Sinussatz hingegen gilt in einem beliebigen Dreieck.Der Sinus eines Winkels eines rechtwinkligen Dreiecks ist das Verhältnis seiner Senkrechten (also dem Winkel entgegengesetzt) ​​zur Hypotenuse. Die Sündenformel lautet: sin θ = Senkrechte / Hypotenuse . sin(θ + 2nπ) = sin θ für jedes θ

Was besagt der Sinussatz

• müssen mindestens 3 Größen (Seitenlängen bzw. Winkel) bekannt sein und.
• unter den gegebenen Größen müssen eine Seitenlänge und der gegenüberliegende Winkel sein.

Wie löst man schiefe Dreiecke mit dem Sinusgesetz : Das Sinusgesetz

Wenn Sie zunächst zwei Winkel und die Seite kennen, die einem dieser Winkel gegenüberliegt, können Sie die Seite bestimmen, die dem anderen Winkel gegenüberliegt . Wenn beispielsweise Winkel A = 30°, Winkel B = 45° und Seite a = 16, dann lautet das Sinusgesetz (sin 30°)/16 = (sin 45°)/b.

Wie löst man ein Dreieck mit einem Winkel und zwei Seiten : Wenn Sie zunächst einen Winkel und die beiden angrenzenden Seiten kennen, können Sie die gegenüberliegende Seite bestimmen . Wenn beispielsweise der Winkel C = 60°, die Seite a = 5 und die Seite b = 8 ist, dann lautet das Kosinusgesetz: c 2 = 25 + 64 – 80 cos 60°. Da der Kosinus von 60° 1/2 beträgt, vereinfacht sich diese Gleichung zu c 2 = 49, also c = 7.

Wie finde ich eine Seite mit einem gegebenen Winkel und einer Seite

Wir kennen vielleicht nur eine Seite, aber wir kennen auch einen Winkel. Wenn beispielsweise die Seite a = 15 und der Winkel A = 41° beträgt, können wir einen Sinus und einen Tangens verwenden, um die Hypotenuse und die andere Seite zu ermitteln . Da sin A = a/c ist, wissen wir c = a/sin A = 15/sin 41. Mit einem Taschenrechner ist dies 15/0,6561 = 22,864.

Der Sinus lässt sich nur von »einfachen« Winkeln wie 0°, 30°, 45° oder 60° im Kopf berechnen. Können Sie dennoch ohne Taschenrechner, Smartphone oder Computer die Summe sin2(1°) + sin2(2°) + sin2(3°) + …Wir können das Sinusgesetz verwenden, um jedes schiefe Dreieck zu lösen , aber einige Lösungen sind möglicherweise nicht einfach. In einigen Fällen erfüllen möglicherweise mehr als ein Dreieck die angegebenen Kriterien, was wir als mehrdeutigen Fall bezeichnen.

Kann man ein Dreieck mit einer Seite und einem Winkel lösen : Wir kennen vielleicht nur eine Seite, aber wir kennen auch einen Winkel. Wenn beispielsweise die Seite a = 15 und der Winkel A = 41° beträgt, können wir einen Sinus und einen Tangens verwenden, um die Hypotenuse und die andere Seite zu ermitteln . Da sin A = a/c ist, wissen wir c = a/sin A = 15/sin 41.